Feature Selection, Dimensionality Reduction, and Spot Clustering
Last updated on 2024-06-20 | Edit this page
Overview
Questions
- Why is feature selection important in spatial transcriptomics?
- What are the implications of using different proportions of highly variable genes (HVGs) in data analysis?
- Why is feature selection in spatial transcriptomics not typically necessary with normalization techniques like SCTransform?
- How do PCA and UMAP differ in their approach to dimensionality reduction in spatial transcriptomics?
- What advantages do linear methods like PCA offer before applying nonlinear methods like UMAP?
- How do these dimensionality reduction techniques impact downstream analysis such as clustering and visualization?
Objectives
- Identify appropriate feature selection methods for different normalization techniques in spatial transcriptomics.
- Evaluate the effects of varying the proportion of highly variable genes on the resolution of clustering and PCA outcomes.
- Understand the rationale behind the dependency of feature selection on specific normalization methods like NormalizeData.
- Differentiate between linear and nonlinear dimensionality reduction methods and their applications in spatial transcriptomics.
- Implement PCA to preprocess data before applying UMAP to enhance interpretability and structure recognition.
- Assess the effectiveness of each method in revealing spatial and molecular patterns within the data.
Understanding the Morphology of your Tissue.
In any analysis, it is important that you understand the structure and cell types in the tissue which you are analyzing. While it would be ideal to have an unbiased analysis that uses normalizations and clustering methods to automatically assign cell types and define tissue structure, in practice we adjust these parameters based on the tissue structure that we expect to find.
Understanding Feature Selection in Spatial Transcriptomics
Feature selection in spatial transcriptomics is essential for reducing the dimensionality of high-dimensional datasets, enhancing model performance, and improving interpretability. This process is crucial because it helps in minimizing computational demands, reducing noise, and speeding up downstream analyses like clustering and PCA. By focusing on a subset of genes that show significant variability or are biologically relevant, researchers can achieve more robust and generalizable models, draw clearer conclusions, and facilitate hypothesis testing.
Choosing Feature Selection Methods
Importance of High Variable Gene Selection
Feature selection methods such as variance stabilizing transformation (VST) and mean-variance plotting are crucial for refining the dataset to include genes that exhibit meaningful variability across different spatial regions. These methods help focus on genes that are most informative for downstream analyses like clustering and dimensionality reduction.
Feature Selection with NormalizeData
When using normalization methods like NormalizeData, which focuses on scaling gene expression data without variance stabilization, applying feature selection becomes essential. This method requires the selection of highly variable genes to enhance the analysis, particularly in clustering and principal component analysis (PCA). Typically, you will select in the range of 2,000 to 5,000 highly variable genes.
Feature Selection with SCTransform
SCTransform, a normalization method, adjusts gene expression data to stabilize the variance, and it also provides default feature selection. This method ensures that the genes retained are already adjusted for technical variability, highlighting those with biological significance.
The SCTransform selects 3,000 variable features by default. We will use those variable features to calculate principal components (PCs) of the gene expression data. As always, we must first scale (or standardize) the normalized counts data.
Too few variable genes may underestimate the variance between spots and tissue sections and would reduce our ability to discern tissue structure. Too many variable genes would increase computational time and might add noise to the analysis.
Dimensionality Reduction using Principal Components
Dimensionality reduction is a crucial step in managing high-dimensional spatial transcriptomics data, enhancing analytical clarity, and reducing computational load. Linear methods like PCA and nonlinear methods like UMAP each play distinct roles in processing and interpreting complex datasets.
Principal Component Analysis (PCA) is a linear technique that reduces dimensionality by transforming data into a set of uncorrelated variables called “principal components” (PCs). This method efficiently captures the main variance in the data, which is vital for preliminary data exploration and noise reduction.
In order to cluster the spots by similarity, we use principal components (PCs) to reduce the number of dimensions in the data. Using a smaller number of PCs allows us to capture the variability in the data set while using a smaller number of dimensions. The PCs are then used to cluster the spots by similarity.
R
filter_st <- ScaleData(filter_st) %>%
RunPCA(npcs = 75, verbose = FALSE)
OUTPUT
Centering and scaling data matrixIn the command above, we specified asked Seurat to calculate 75 principal components. There are thousands of genes and we know that we don’t need to calculate all PCs. By default, the RunPCA method calculates 50 PCs. Let’s make an elbow plot of the number of PCs versus the standard deviation explained by each PC. Traditionally, there is a bend in the curve which indicates that adding more PCs doesn’t account for more of the variance.
R
ElbowPlot(filter_st, ndims = 75)
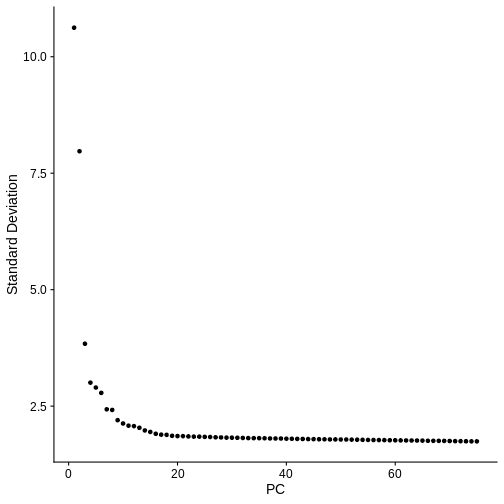
From the plot above, we would normally select somewhere between 10 and 20 PCs because there seems to be little benefit in adding more PCs. Adding more PCs does not seem to add more explanatory variance.
But in spatial transcriptomics, the elbow plot often does not tell the whole story. We want to select a number of PCs such that we are able to discern the structure and cell type composition of our tissue. So it is better to try a range of number of PCs.
For now, let’s use all 75 PCs.
R
n_pcs = 75
In the next step, we will cluster the spots based on expression similarity using the principal components that we just generated. We will use Seurat’s FindNeighbors and FindClusters functions. FindNeighbors find the K nearest neighbors of each spot in the data set. The default values is to use the 20 nearest neighbors in the data set and we will use this value in this lesson. However, as with the number of features used to create the PCs, this is another parameter that is worth varying before proceeding with your analysis.
R
filter_st <- FindNeighbors(filter_st,
reduction = "pca",
dims = 1:n_pcs) %>%
FindClusters(resolution = 1)
OUTPUT
Computing nearest neighbor graphOUTPUT
Computing SNNOUTPUT
Modularity Optimizer version 1.3.0 by Ludo Waltman and Nees Jan van Eck
Number of nodes: 3633
Number of edges: 187716
Running Louvain algorithm...
Maximum modularity in 10 random starts: 0.7178
Number of communities: 9
Elapsed time: 0 secondsThe clustering has added a new column to the spot metadata in the Seurat object called “seurat_clusters”. Let’s look the metadata to see this.
R
head(filter_st[[]])
OUTPUT
orig.ident nCount_Spatial nFeature_Spatial in_tissue
AAACAAGTATCTCCCA-1 SeuratProject 8458 3586 1
AAACAATCTACTAGCA-1 SeuratProject 1667 1150 1
AAACACCAATAACTGC-1 SeuratProject 3769 1960 1
AAACAGAGCGACTCCT-1 SeuratProject 5433 2424 1
AAACAGCTTTCAGAAG-1 SeuratProject 4278 2264 1
AAACAGGGTCTATATT-1 SeuratProject 4004 2178 1
array_row array_col pxl_row_in_fullres pxl_col_in_fullres
AAACAAGTATCTCCCA-1 50 102 8468 9791
AAACAATCTACTAGCA-1 3 43 2807 5769
AAACACCAATAACTGC-1 59 19 9505 4068
AAACAGAGCGACTCCT-1 14 94 4151 9271
AAACAGCTTTCAGAAG-1 43 9 7583 3393
AAACAGGGTCTATATT-1 47 13 8064 3665
percent.mt keep keep_counts layer_guess cell_count
AAACAAGTATCTCCCA-1 16.63514 TRUE TRUE Layer3 6
AAACAATCTACTAGCA-1 12.23755 TRUE FALSE Layer1 16
AAACACCAATAACTGC-1 11.40886 TRUE TRUE WM 5
AAACAGAGCGACTCCT-1 24.22234 TRUE TRUE Layer3 2
AAACAGCTTTCAGAAG-1 15.21739 TRUE TRUE Layer5 4
AAACAGGGTCTATATT-1 15.50949 TRUE TRUE Layer6 6
nCount_SCT nFeature_SCT SCT_snn_res.1 seurat_clusters
AAACAAGTATCTCCCA-1 5159 3183 1 1
AAACAATCTACTAGCA-1 3400 1264 4 4
AAACACCAATAACTGC-1 3828 1941 6 6
AAACAGAGCGACTCCT-1 4682 2393 5 5
AAACAGCTTTCAGAAG-1 4228 2239 0 0
AAACAGGGTCTATATT-1 3991 2148 3 3We previously discussed the layer annotations provided by Maynard and colleagues. We added them to our Seurat object and plotted them. Let’s look at them again to compare them to our clusters.
R
SpatialDimPlotColorSafe(filter_st[, !is.na(filter_st[[]]$layer_guess)], "layer_guess") + labs(fill="Layer")
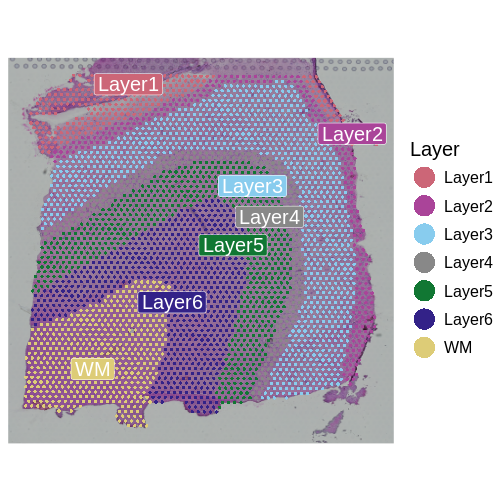
The authors describe six layers arranged from the upper right to the lower left, and a white matter (WM) later. At this stage of the analysis, we have nine clusters, but they do not show the clear separation of the ground truch in the source publication.
We will now plot the spots in the tissue, colored by the clusters which we have identified in “seurat_clusters” to evaluate the quality of the cluster identities by looking for the clarity of the stripes forming each layer.
R
SpatialDimPlotColorSafe(filter_st, "seurat_clusters") + labs(fill="Cluster")
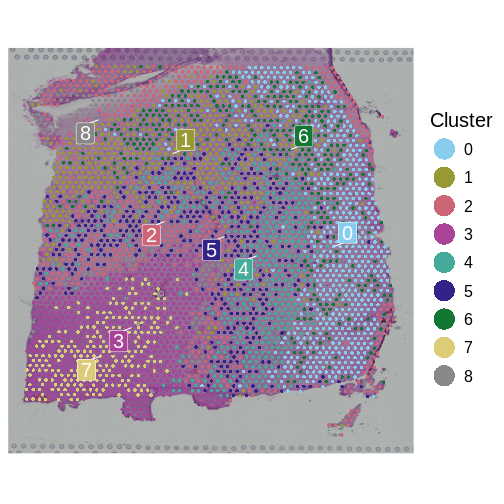
How many layers do we have compared to the publication? What do you think about the quality of the layers in this plot? Are there clear layers in the tissue?
Another way for us to look at the clusters it to plot them in a Uniform Manifold Approximation and Projection (UMAP). UMAP is a non-linear dimension reduction technique that can be used to visualize data. This is often used in single-cell RNASeq to identify different cell types. Here, each spot is potentially composed of more than one cell type, so the clustering may not be as clear.
R
num_clusters <- length(unique(filter_st[[]]$seurat_clusters))
color_pal <- setNames(carto_pal(num_clusters, "Safe"), 0:(num_clusters - 1))
filter_st <- RunUMAP(filter_st,
reduction = 'pca',
dims = 1:n_pcs,
verbose = FALSE)
UMAPPlot(filter_st,
label = TRUE,
cols = color_pal,
pt.size = 2,
label.size = 6)
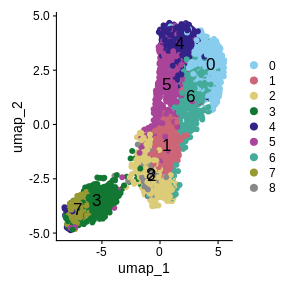
We have made some decisions above which might affect the quality of out spot clusters, including the number of nearest neighbors, the number of variable features, the number of PCs, and the cluster resolution. As we have mentioned, it is critical to have some understanding of the structure of the tissue that you are analyzing. In the absence of “ground truth”, you will need to try several different parameters and look at how the clusters group in your tissue. Below, we have included code which plots the tissue with different numbers of nearest neighbors, principal components, and cluster resolutions. We will not run this code because it takes a long time to run, but we show the output below this code block.
R
# Set several cluster resolution values.
resol <- c(0.5, 1, 2)
# Set several numbers of principal components.
npcs <- c(25, 50, 75)
num_clusters <- 12
color_pal <- setNames(carto_pal(num_clusters, "Safe"), 0:(num_clusters - 1))
umap_plots <- vector('list', length(resol) * length(npcs))
plots <- vector('list', length(resol) * length(npcs))
for(i in seq_along(resol)) {
for(j in seq_along(npcs)) {
index <- (i-1) * length(npcs) + j
print(paste('Index =', index))
filter_st <- FindNeighbors(filter_st,
reduction = "pca",
dims = 1:npcs[j]) %>%
FindClusters(resolution = resol[i]) %>%
RunUMAP(reduction = 'pca',
dims = 1:npcs[j],
verbose = FALSE)
umap_plots[[index]] <- UMAPPlot(filter_st, label = TRUE, cols = color_pal,
pt.size = 2, label.size = 4) +
ggtitle(paste("res =", resol[i], ": pc =", npcs[j])) +
theme(legend.position = "none")
plots[[index]] <- SpatialDimPlot(filter_st, group.by = "seurat_clusters", cols = color_pal) +
ggtitle(paste("res =", resol[i], ": pc =", npcs[j])) +
theme(legend.position = "none")
} # for(j)
} # for(i)
png(file.path('episodes', 'fig', 'tissue_cluster_resol.png'),
width = 1000, height = 1000, res = 128)
print(gridExtra::grid.arrange(grobs = plots, nrow = 3))
dev.off()
png(file.path('episodes', 'fig', 'umap_cluster_resol.png'),
width = 1000, height = 1000, res = 128)
print(gridExtra::grid.arrange(grobs = umap_plots, nrow = 3))
dev.off()
The plot below shows the clusters as colors overlayed on the tissue. Each row shows a different cluster resolutions and each column snows the number of PCs.
The plot below shows the UMAP clustering for the same set of parameters in the same order. The cluster colors are the same in the plots above and below. Increasing the cluster resolution increases the number of clusters.
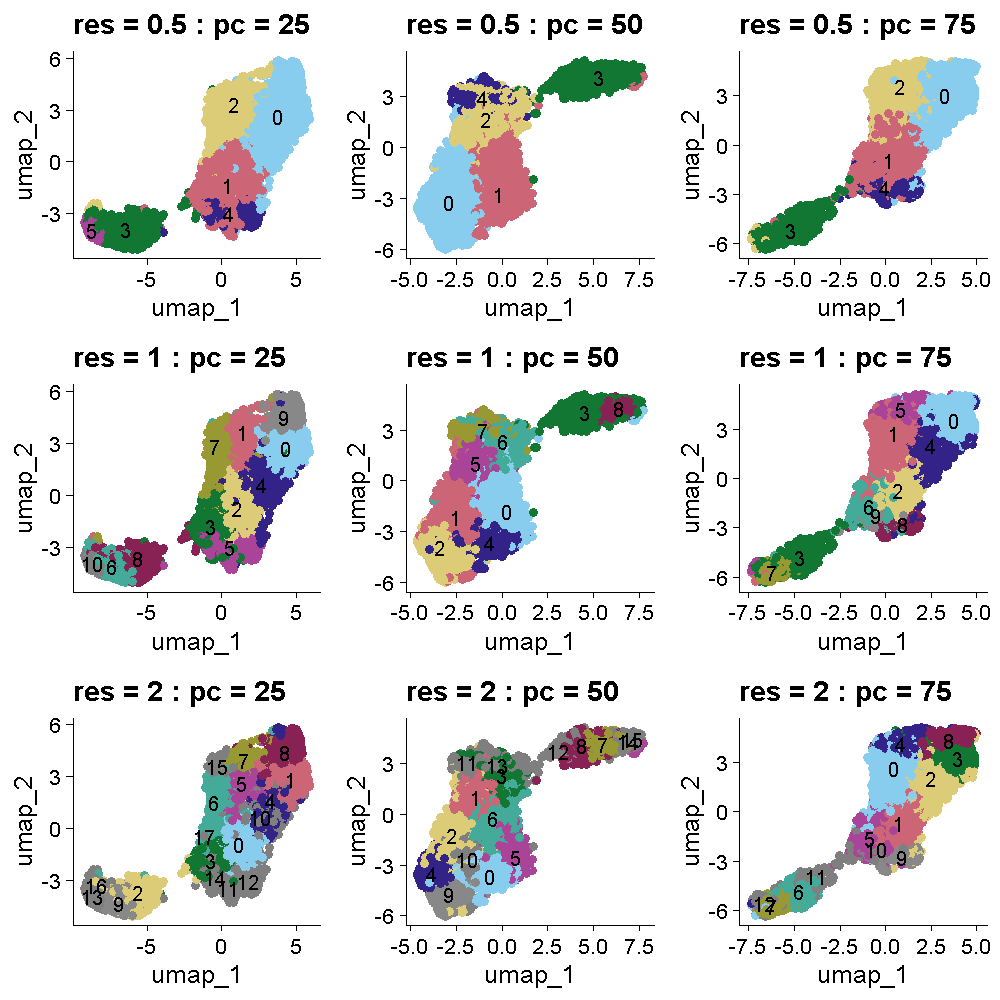
Challenge 1: Select cluster resolution and number of PCs.
Look at the two plots above which show the tissue and UMAP clusters at different cluster resolutions and number of PCs. Think about which settings seem to produce clustering that matches the expectations from the publication. Turn to the person next to you and discuss your opinions about which settings to use.
All of the plots in the tissue clustering show layers which broadly conform to the publication’s “ground truth.” In the top row at a resolution of 0.5, we see about four layers with varying levels of clarity, depending on the number of PCs. As we move down in the tissue clustering plot, the layers become clearer at a resolution of 1, but then become less clear at a resolution of 2 in the bottom row. When we look at the corresponding row in the UMAP plots, we see that the white matter is clearly separated in all of the plots. The number of clusters increases with increasing cluster resolution, with the middle row (cluster resolution = 1), having close to seven layers, like the publication ground truth. The middle plot in the middle row has nine clusters, which is also close to the publication.
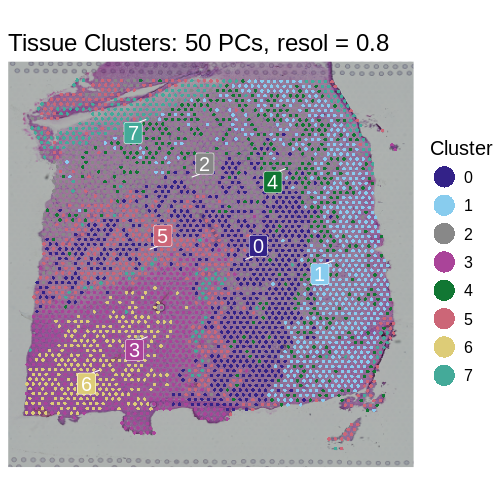
We selected a cluster resolution of 0.8 and 50 PCs for the following work.
R
filter_st <- FindNeighbors(filter_st,
reduction = "pca",
dims = 1:50) %>%
FindClusters(resolution = 0.8)
OUTPUT
Modularity Optimizer version 1.3.0 by Ludo Waltman and Nees Jan van Eck
Number of nodes: 3633
Number of edges: 171945
Running Louvain algorithm...
Maximum modularity in 10 random starts: 0.7408
Number of communities: 9
Elapsed time: 0 secondsR
SpatialDimPlotColorSafe(filter_st, "seurat_clusters") +
ggtitle(label = "Tissue Clusters: 50 PCs, resol = 0.8") +
labs(fill = "Cluster")
Key Points
- Feature selection is a crucial step in spatial transcriptomics analysis, particularly for non-variance-stabilizing normalization methods like NormalizeData.
- Techniques such as VST and mean-variance plotting enable researchers to focus on genes that provide the most biological insight.
- Different proportions of highly variable genes and feature selection methods can significantly influence the analytical outcomes, emphasizing the need for tailored approaches based on the specific characteristics of each dataset.
- Linear dimensionality reduction methods like PCA are crucial for initial data simplification and noise reduction.
- Nonlinear methods like UMAP are valuable for detailed exploration of data structures post-linear preprocessing.
- The sequential application of PCA and UMAP can provide a comprehensive view of the spatial transcriptomics data, leveraging the strengths of both linear and nonlinear approaches.