Performing a genome scan with a linear mixed model

Overview

Questions

• How do I use a linear mixed model in a genome scan?
• How do different mapping and kinship calculation methods differ?

Objectives

• Create a genome scan with a linear mixed model.
• Compare LOD plots for Haley-Knott regression and linear mixed model methods.
• Compare LOD plots for the standard kinship matrix with the leave-one-chromosome-out (LOCO) method.

Genetic mapping in mice presents a good example of why accounting for population structure is important.

Geographical ranges of subspecies in the Mus musculus group. From Mouse Genetics: Concepts and Applications by Lee M. Silver, Oxford University Press, 1995.

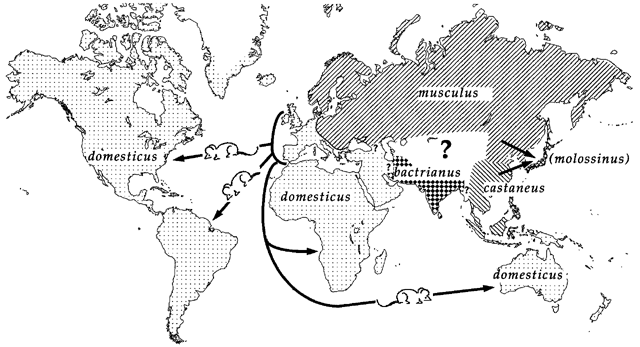
Laboratory mouse strains are descended from a small number of founders (fancy mice) and went through several population bottlenecks.

The genealogy of inbred mice. From Origins of Inbred Mice edited by Herbert C. Morse III, Academic Press, 1978. Permission from Elsevier.

Wild-derived strains are not descended from fancy mice and don’t share the same history as laboratory strains.

Issues of population structure and differing degrees of genetic relatedness between mice are addressed using linear mixed models (LMM). LMMs consider genome-wide similarity between all pairs of individuals to account for population structure, known kinship and unknown relatedness. LMMs in mapping studies can successfully adjust for genetic relatedness between individuals in a population by incorporating kinship into the model. Earlier we calculated a kinship matrix for input to a linear mixed model to account for relationships among individuals. For a current review of mixed models in genetics, see Sul et al, PLoS Genetics, 2018.

Simple linear regression takes the form:

\(y = \mu + \beta G + \epsilon\)

which describes a line with slope \(\beta\) and y-intercept \(\mu\). The error (or residual) is represented by \(\epsilon\).

To model the relationship between the phenotype \(y\) and the genotypes at one marker, we use:

\(y_j = \mu + \beta_k G_{jk} + \epsilon_j\)

where \(y_j\) is the phenotype of the \(j\)th individual, \(\mu\) is the mean phenotype value, \(\beta_k\) is the effect of the \(k\)th genotype, \(G_{jk}\) is the genotype for individual \(j\), and \(\epsilon_j\) is the error for the \(j\)th individual. In the figure below, \(\mu\) equals 94.6 and \(\beta\) equals 15 for the alternative hypothesis (QTL exists). This linear model is \(y\) = 94.6 + 15\(G\) + \(\epsilon\). The model intersects the genotype groups at their group means. In contrast, the null hypothesis would state that there is no difference in group means (no QTL anywhere). The linear model for the null hypothesis would be \(y\) = 94.6 + 0\(G\) + \(\epsilon\). This states that the phenotype is equal to the combined mean (94.6), plus some error (\(\epsilon\)). In other words, genotype doesn’t affect the phenotype.

Null and Alternative Hypotheses

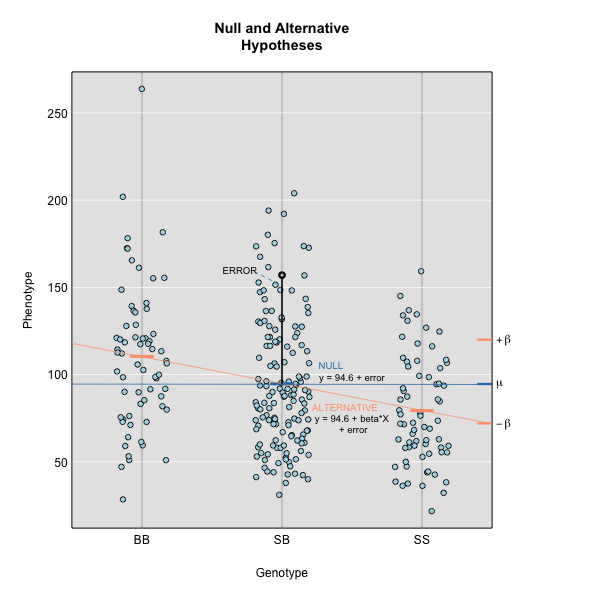
The linear models above describe the relationship between genotype and phenotype but are inadequate for describing the relationship between genotype and phenotype in large datasets. They don’t account for relatedness among individuals. In real populations, the effect of a single genotype is influenced by many other genotypes that affect the phenotype. A true genetic model takes into account the effect of all variants on the phenotype.

To model the phenotypes of all individuals in the data, we can adapt the simple linear model to include all individuals and their variants so that we capture the effect of all variants shared by individuals on their phenotypes.

\(y=\mu+\sum_{i=1}^M{\beta_iG_i}+\epsilon\)

Now, \(y\) represents the phenotypes of all individuals. The effect of the \(i\)th genotype on the phenotype is \(\beta_i\), the mean is \(\mu\) and the error is \(\epsilon\). Here, the number of genotypes is M.

To model the effect of all genotypes and to account for relatedness, we test the effect of a single genotype while bringing all other genotypes into the model.

\(y=\mu + \beta_kG_k +\sum_{i\neq k}^{M}\beta_iG_i + \epsilon\)

\(\beta_k\) is the effect of the genotype \(G_k\), and \(\sum_{i\neq k}^{M}\beta_iG_i\) sums the effects across all markers (M) of all other genotypes except genotype \(k\). For the leave one chromosome out (LOCO) method, \(\beta_kG_k\) is the effect of genotypes on chromosome \(k\), and \(\beta_iG_i\) represents the effects of genotypes on all other chromosomes.

If the sample contains divergent subpopulations, SNPs on different chromosomes will be correlated because of the difference in allele frequencies between subpopulations caused by relatedness. To correct for correlations between chromosomes, we model all genotypes on the other chromosomes when testing for the association of a SNP.

First, we will create a single kinship matrix using all of the genotype probabilities on all chromosomes.

R

kinship_all <- calc_kinship(probs = probs, 
                            type = "overall")

To perform a genome scan using a linear mixed model you also use the function scan1; you just need to provide the argument kinship, a kinship matrix (or, for the LOCO method, a list of kinship matrices).

R

lod_add_all <- scan1(genoprobs = probs, 
                     pheno     = insulin, 
                     kinship   = kinship_all, 
                     addcovar  = addcovar)

Again, on a multi-core machine, you can get some speed-up using the cores argument.

R

lod_add_all <- scan1(genoprobs = probs, 
                     pheno     = insulin, 
                     kinship   = kinship_all, 
                     addcovar  = addcovar, 
                     cores     = 4)

Let’s plot the insulin genome scan using the overall kinship matrix.

R

plot_scan1(x     = lod_add,  
           map   = cross$pmap,
           col   = 'black',
           main  = "log10(insulin): Kinship Comparison")
plot_scan1(x     = lod_add_all,  
           map   = cross$pmap,
           col   = 'blue',
           add   = TRUE)
legend(x = 1000, y = max(lod_add), legend = c('No kinship', 'Overall kinship'), 
       col = c('black', 'blue'), lwd = 2)

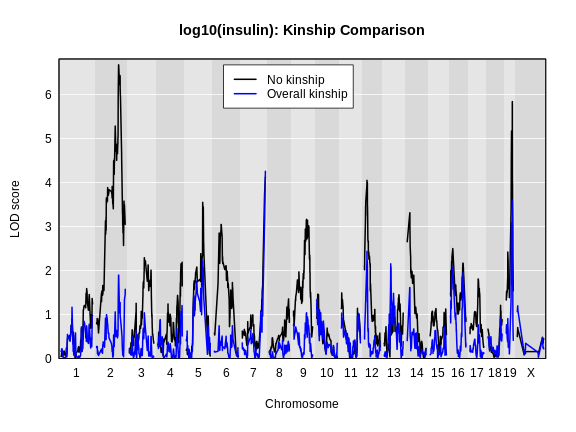
How did the LOD scores change? Did they increase or decrease? In general, the LOD scores decreased. In some cases, the LOD score decreased drastically. Why would this happen?

To answer this, we have to think back to the mapping model that we are using.

\(y=\mu + \beta_kG_k +\sum_{i}^{M}\beta_iG_i + \epsilon\)

In this model, we explicitly excluded the current marker from the kinship calculation. However, when we calculated the kinship matrix above, we used ALL of the markers. This means that we have put the current marker \(k\) into the model twice. This causes a loss of power which has been reported in Yang et al., Nat. Gen., 2014.

In order to address this issue, we could remove the current marker from the calculation. But this would mean that we would have to calculate a different kinship matrix for every marker. As a compromise, researchers create a different kinship matrix for each chromosome which uses all of the markers except those on the current chromosome. For example, to create a kinship matrix to use on chromosome 1, we would use the markers on chromosomes 2 through X. This is called the Leave One Chromosome Out (LOCO) method.

The LOCO mapping method is shown conceptually by the equation below:

\(y=\mu + \beta_kG_k +\sum_{i\neq k}^{M}\beta_iG_i + \epsilon\)

Note that we use all markers except the current marker being mapped. As we mentioned above, in practice, we exclude the chromosome of the current marker from the kinship matrix calculation.

In order to use the LOCO method (scan each chromosome using a kinship matrix that is calculated using data from all other chromosomes), use type="loco" in the call to calc_kinship().

R

kinship_loco <- calc_kinship(probs = probs, 
                             type  = "loco")

For the LOCO (leave one chromosome out) method, provide the list of kinship matrices as obtained from calc_kinship() with type="loco".

R

lod_add_loco <- scan1(genoprobs = probs, 
                      pheno     = insulin, 
                      kinship   = kinship_loco, 
                      addcovar  = addcovar)

To plot the results, we again use plot_scan1().

Here is a plot of the LOD scores by Haley-Knott regression and the linear mixed model using either the standard kinship matrix or the LOCO method.

R

plot_scan1(x     = lod_add,      
           map   = cross$pmap, 
           col   = 'black',
           ylim  = c(0, 7.5))
plot_scan1(x     = lod_add_all,  
           map   = cross$pmap, 
           col   = 'blue',   
           add   = TRUE)
plot_scan1(x     = lod_add_loco, 
           map   = cross$pmap, 
           col   = 'darkgreen', 
           add   = TRUE)
legend(x = 1500, y = 7.5, legend = c("No kinship", "All kinship", "LOCO kinship"),
       lwd = 2, col = c('black', 'blue', 'darkgreen'))

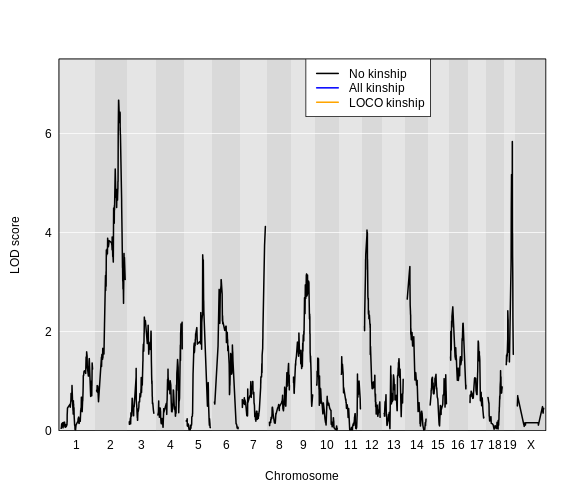
For circulating insulin, the three methods give quite different results. The linear mixed model with an overall kinship matrix (blue) produces much lower LOD scores than the other two methods. On chromosomes with some evidence of a QTL, the LOCO method gives higher LOD scores than Haley-Knott, except on chromosome 6 where it gives lower LOD scores.

Let’s plot the difference between the LOCO-kinship genome scan and the no-kinship genome scan.

R

plot(x    = lod_add_loco - lod_add, 
     map  = cross$pmap, 
     ylim = c(-1.5, 2),
     main = "LOCO - no kinship Genome Scan")

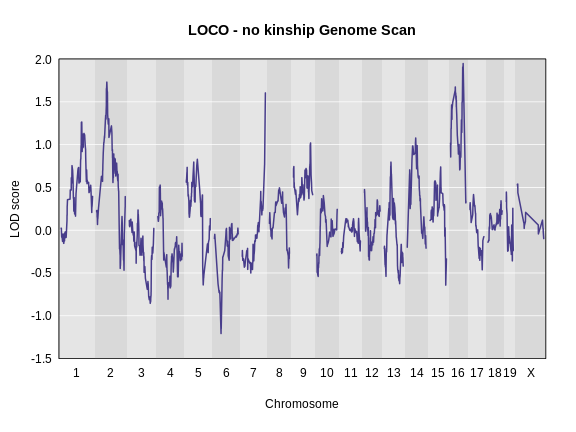
As you can see from the plot above, the LOCO-kinship scan generally produces higher LOD scores. While higher LOD scores don’t always mean that the model is better, in this case, we expect that accounting for the correlation in residual errors using kinship matrices will produce more correct results.

Challenge 1

What are the benefits and disadvantages of the three methods for genome scanning (Haley-Knott regression, kinship matrix, and leave-one-chromosome out (LOCO)?)
Which method would you use to scan, and why?
Think about the advantages and disadvantages of each, discuss with a neighbor, and share your thoughts in the collaborative document.

Show me the solution

Haley-Knott regression does not consider the kinship between mice. This may increase or decrease the LOD score and least to false or missed discoveries. Including a kinship matrix which uses all of the markers in the mapping model causes a loss of power because the marker is fit twice in the model. A compromise approach is to create a separate kinship matrix for each chromosome which uses all of the markers expect those on the current chromosome. This estimates kinship while preventing the current marker from being in the model twice. The LOCO method leads to better power to identify QTL.

Challenge 2: Pair programming

With a partner, review and carry out all of the steps in QTL mapping that we have covered so far, using a new data set. One of you types the code, the other explains what needs to happen next, finds the relevant code in the lesson, suggests new names for objects (i.e. NOT the ones you’ve already used, such as map, pr, out, prob, etc.).

1. Load the Gough data into an object called gough. You can find code to load the data at the bottom of the page.
2. Calculate genotype probabilities.
3. Run a genome scan for the first 16 phenotypes using pheno = gough$pheno[, 1:16]. These represent 16 weeks of body weight measurements. The remaining phenotypes are derivations of these measurements.
4. Calculate a kinship matrix.
5. Calculate a list of kinship matrices with the LOCO method.
6. Run genome scans with the regular kinship matrix and with the list of LOCO matrices.
7. Plot the 3 different genome scans in a single plot in different colors. By default, the plot() function will give you the first lod column which is for week 1. You can add the lodcolumn = argument to the call to plot and insert additional lod column numbers up to 16.
8. Which chromosomes appear to have peaks with a LOD score greater than 7? Which methods identify these peaks? Which don’t?

Show me the solution

file <- paste0("https://raw.githubusercontent.com/rqtl/", "qtl2data/main/Gough/gough.zip")
gough <- read_cross2(file)
summary(gough)
head(goughpheno)
colnames(gough$pheno)
goughmap <- gough$pmap
prgough <- calc_genoprob(cross=gough, map=goughmap, error_prob=0.002)
goughaddcovar <- get_x_covar(gough)
goughscan <- scan1(genoprobs = prgough, pheno = gough$pheno[, 1:16], addcovar=goughaddcovar)
plot(goughscan, map = goughmap)
goughkinship <- calc_kinship(probs = prgough)
out_pg_gough <- scan1(prgough, bgough$pheno, kinship=goughkinship, addcovar=goughaddcovar)
kinship_loco_gough <- calc_kinship(prgough, "loco")
out_pg_loco_gough <- scan1(prgough, gough$pheno, kinship_loco_gough, addcovar=goughaddcovar)
plot_scan1(out_pg_loco_gough, map = goughmap, lodcolumn = 2, col = "black")
plot_scan1(out_pg_gough, map = goughmap, lodcolumn = 2, col = "blue", add = TRUE)
plot_scan1(goughscan, map = goughmap, lodcolumn = 2, col = "green", add = TRUE)

Key Points

• To perform a genome scan with a linear mixed model, supply a kinship matrix.
• Different mapping and kinship calculation methods give different results.
• Using a set of Leave-One-Chromosome-Out kinship matrices generally produces higher LOD scores than other methods.